6.3Class-Prediction for New Instances
New email does not come with a label ham or spam (if it would we could throw spam in the spam-box right away). What we do see are the attributes{X__i}. Our task is to guess the label based on the model and the measured attributes. The approach we take is simple: calculate whether the email has a higher probability of being generated from the spam or the ham model. For example, because the word “viagra” has a tiny probability of being generated under the ham model it will end up with a higher probability under the spam model. But clearly, all words have a say in this process. It’s like a large committee of experts, one for each word. each member casts a vote and can say things like:“I am 99% certain its spam”, or “It’s almost definitely not spam (0.1% spam)”. Each of these opinions will be multiplied together to generate a final score. We then figure out whether ham or spam has the highest score.
There is one little practical caveat with this approach, namely that the product of a large number of probabilities, each of which is necessarily smaller than one, very quickly gets so small that your computer can’t handle it. There is an easy fix though.Instead of multiplying probabilities as scores, we use the logarithms of those probabilities and add the logarithms. This is numerically stable and leads to the same conclusion because ifa > b_then we also have thatlog(_a)>_log(_b)and vice versa. In equations we compute the score as follows:
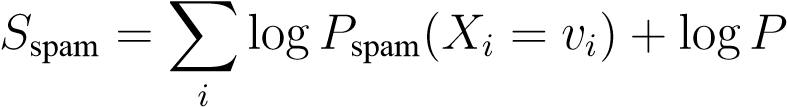 (spam)(6.7)
(spam)(6.7)
6.3. CLASS-PREDICTIONFORNEWINSTANCES
where with_v__i_we mean the value for attribute_i_that we observe in the email under consideration, i.e. if the email contains no mention of the word “viagra” we set_v_viagra= 0.
The first term in Eqn.6.7 adds all the log-probabilities under the spam model of observing the particular value of each attribute. Every time a word is observed that has high probability for the spam model, and hence has often been observed inthe dataset, will boost this score. The last term adds an extra factor to the score that expresses our prior belief of receiving a spam email instead of a ham email. We compute a similar score for ham, namely,
S_ham= Xlog_P_ham(_X__i=v__i) + logP(ham)(6.8)
i
and compare the two scores. Clearly, a large score for spam relative to ham provides evidence that the email is indeed spam. If your goal is to minimize the total number of errors (whether they involve spam or ham) then the decision should be to choose theclass which has the highest score.
In reality, one type of error could have more serious consequences than another. For instance, a spam email making it in my inbox is not too bad, bad an important email that ends up in my spam-box (which I never check) may have serious consequences. To account for this we introduce a general threshold_θ_and
| use the following decision rule, | ||
|---|---|---|
| Y= 1 | ifS_1> S0+θ_ | (6.9) |
| Y= 0 | ifS_1< S0+θ_ | (6.10) |
(6.11)
If these quantities are equal you flip a coin.
Ifθ= −∞, we always decide in favor of labelY= 1, while if we useθ= +∞we always decide in favor ofY= 0. The actual value is a matter of taste. To evaluate a classifier we often draw an ROC curve. An ROC curve is obtained by slidingθ_between−∞and+∞and plotting the true positive rate (the number of examples with label_Y= 1also classified asY= 1divided by the total number of examples withY= 1) versus the false positive rate (the number of examples with labelY= 0classified asY= 1divided by thetotal number of examples withY= 0). For more details see chapter??.