59

CHAPTER12. KERNELPRINCIPALCOMPONENTSANALYSIS

tained eigen-directions of largest variance:

(12.2)

whereU__k_means the_d×_k_sub-matrix containingthe first_k_eigenvectors as columns. As a side effect, we can now show that the projected data are de-correlated in this new basis:

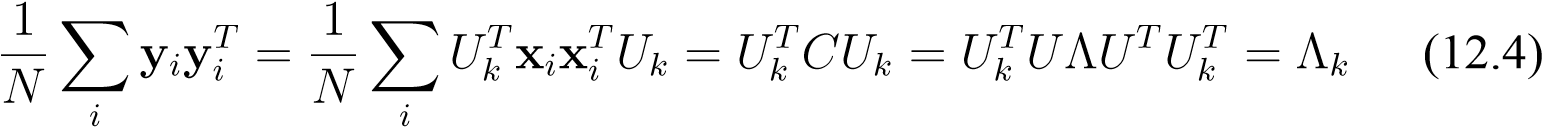
whereΛk_is the (diagonal)_k×_k_sub-matrix corresponding to the largest eigenvalues.

Another convenient property of this procedure isthat the reconstruction error in_L_2-norm between fromytoxis minimal, i.e.

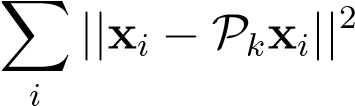(12.5)

wherePk=UkUkT_is the projection onto the subspace spanned by the columns of_U__k, is minimal.

Now imagine that there are more dimensions than data-cases, i.e. some dimensions remain unoccupied by the data. In this case it is not hard to show that the eigen-vectors that span the projection space must lie in the subspace spanned by the data-cases. This can be seen as follows,

xi

_i_ii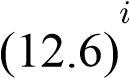

whereua_is some arbitrary eigen-vector of_C. The last expression can be interpreted as: “every eigen-vector can be exactly written (i.e. losslessly) as some linear combination of the data-vectors, and hence it must lie in its span”. This also implies that instead of the eigenvalue equationsCu=λuwe may consider the_N_projected equationsx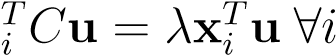. From this equation the coefficients

12.1. CENTERINGDATAINFEATURESPACE61

αia_can be computed efficiently a space of dimension_N(and notd) as follows,

x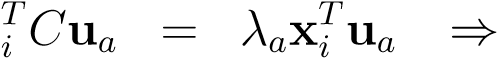

x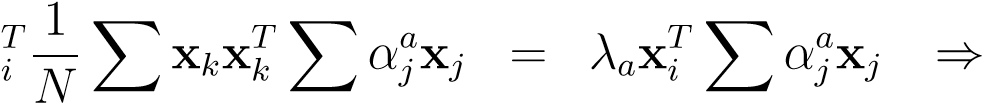

_k_jj

1_a_TTaT

N_Xαj[x_ixk][xkxj]=_λaXα_jxixj

_j,k_j

We now rename the matrix[xT__ixj] =_K__ij_to arrive at,

K_2α_a=NλaKαa⇒Kαa= (λ˜a)αa_withλ˜_a=Nλ__a(12.8)

So, we have derived an eigenvalue equation forαwhich in turn completely determines the eigenvectorsu. By requiring thatuis normalized we find,

u

i,j

(12.9) Finally, when we receive a new data-casetand we like to compute its projections onto the new reduced space, we compute,

u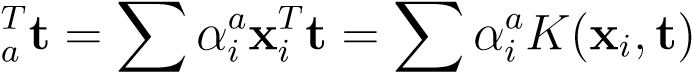(12.10)_i_i

This equation should look familiar, it is central to most kernel methods.

Obviously, the whole exposition was setup so that in the end we only needed the matrixK_to do our calculations. This implies that we are now ready to kernelize the procedure by replacingx_i→ Φ(xi)and definingK__ij= Φ(xi)Φ(xj)T, whereΦ(xi) = Φia.