14.1Kernel CCA

As usual, the starting point to map the data-cases to feature vectorsΦ(xi)andΨ(yi).When the dimensionality of the space is larger than the number of datacases in the training-set, then the solution must lie in the span of data-cases, i.e.

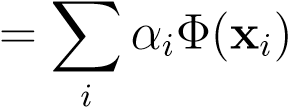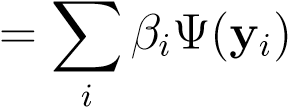ab(14.7)

Using this equation in the Lagrangian we get,

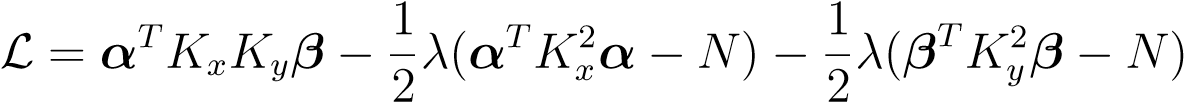(14.8)

whereαis a vector in a differentN-dimensional space than e.g.awhich lives in aD-dimensional space, andK__x=iΦ(xi)TΦ(xi)and similarly forK__y. Taking derivatives w.r.t.αandβPwe find,

KxK__yβ	=		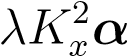(14.9)
KyK__xα	=	_λK__y_2β	(14.10)

Let’s try to solve these equations by assuming thatKx_is full rank (which is typically the case). We get,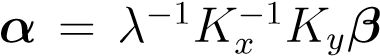and hence,_Ky_2β=λ2_K__y_2βwhich always has a solution forλ_= 1. By recalling that,

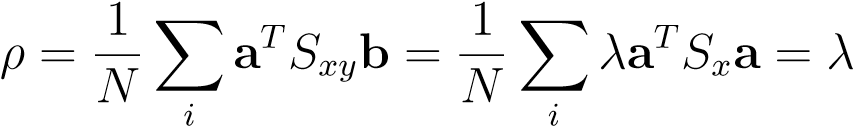(14.11)

we observe that this represents the solution with maximal correlation and hence the preferred one. This is a typical case of over-fitting emphasizes again the need to regularize in kernel methods. This can be done by adding a diagonal term to the constraints in the Lagrangian (or equivalently to the denominator of the original objective), leading to the Lagrangian,

T_1_T_2α+η||α||2−_N) − 1λ(βTKy_2β+η||β||2−_N)

L =αKxK__yβ−λ(αK__x

22

(14.12) One can see that this acts as a quadratic penalty on the norm ofαandβ. The resulting equations are,

CHAPTER14. KERNELCANONICALCORRELATIONANALYSIS

Analogues to the primal problem, we will define big matrices,KD_which contains(_Kx_2+ηI)and(_K__y_2+ηI)as blocks on the diagonal and zeros at the blocks off the diagonal, and the matrix_KO_which has the matrices_KxKy_on the right-upper off diagonal block and_KyK__x_at the left-lower off-diagonal block. Also, we defineγ= [α,_β]. This leads to the equation,

1111

K__Oγ=λK__Dγ⇒K__D−1K__Oγ=λγ⇒KO_2_KD−1KO_2(_KO_2γ) =λ_(_K__O_2γ)

(14.15)

which is again a regular eigenvalue equation. Note that the regularization also moved the smallest eigenvalue away from zero, and hence made the inverse more numerically stable. The value for_η_needs to be chosen using cross-validation or some other measure. Solving the equations using this larger eigen-value problem is actually not quite necessary, and more efficient methods exist (see book).

The solutions are not expected to be sparse,because eigen-vectors are not expected to be sparse. One would have to replace_L_2norm penalties with_L_1norm penalties to obtain sparsity.

Appendix A