63

CHAPTER13. FISHERLINEARDISCRIMINANTANALYSIS

the scatter matrices are:

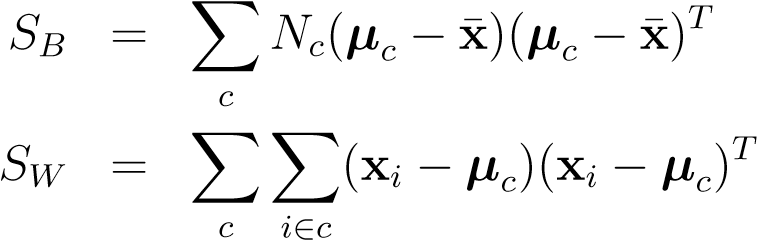(13.2)

(13.3)

where,

1

µ__c=x__i(13.4)

_N__c_X

i∈c

11

x¯ ==x__i=Ncµ__c(13.5)

_N_X_N_X

_i_c

andN__c_is the number of cases in class_c. Oftentimes you will see that for 2 classesSB_is defined as_SB′= (µ1−µ2)(µ1−µ2)T. This is the scatter of class 1 with respect to the scatter of class 2 and you can show that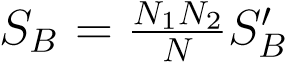, but since it boils down to multiplying the objective with a constant is makes no difference to the final solution.

Why does this objective make sense. Well, itsays that a good solution is one where the class-means are well separated, measured relative to the (sum of the) variances of the data assigned to a particular class. This is precisely what we want, because it implies that the gap between the classes is expected to be big. It is also interesting to observe that since the total scatter,

J(w) =TSWw−1(13.7)w

and hence can be interpreted as maximizing the total scatter of the data while minimizing the within scatter of the classes.

An important property to notice about the objectiveJ_is that is is invariant w.r.t. rescalings of the vectorsw→αw. Hence, we can always choosewsuch that the denominator is simplyw_TSWw= 1, since it is a scalar itself. For this reason we can transform the problem of maximizing J into the following constrained

minw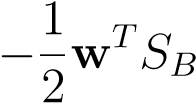w(13.8) s.t.wTSWw= 1(13.9)

corresponding to the lagrangian,

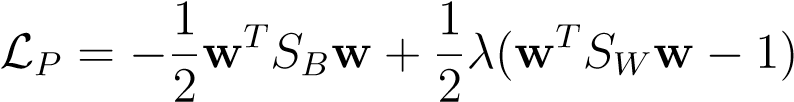(13.10)

(the halves are added for convenience). The KKT conditions tell us that the following equation needs to hold at the solution,

S__Bw=λS__Ww(13.11)

This almost looks like an eigen-value equation. In fact, it is called a generalized eigen-problem and just like an normal eigenvalue problem there are standard ways to solve it.

Remains to choose which eigenvalue and eigenvector corresponds to the desiredsolution. Plugging the solution back into the objectiveJ, we find,

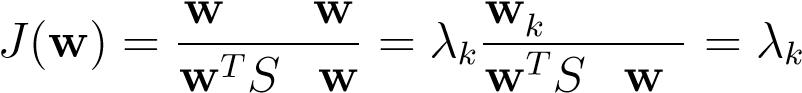TSB_T_S__Wwk

(13.12)

_W_kWk

from which it immediately follows that we want the largest eigenvalue to maximize the objective⁴.

⁴. If you try to find the dual and maximize that, you’ll get the wrong sign it seems. My best guess of what goes wrong is that the constraint is not linear and as a result the problem is not convex and hence we cannot expect the optimal dual solution to be the same as the optimal primal solution. ↩