10.2An alternative derivation
Instead of optimizing the cost function above we can introduce Lagrange multipliers into the problem. This will have the effect that the derivation goes along similar lines as the SVM case. We introduce new variables,ξ__i=y__i−wTΦ_i_and
| rewrite the objective as the following constrained QP, | |||||
|---|---|---|---|---|---|
| minimize−w,ξLP= X_ξ__i_2 | (10.8) | ||||
| w | ≤B | (10.9) |
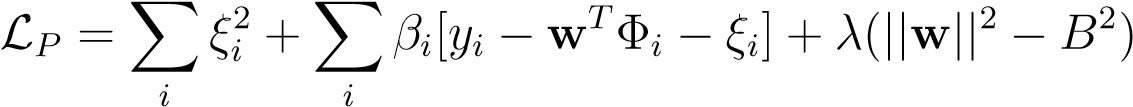 (10.10)
(10.10)
Two of the KKT conditions tell us that at the solution we have:
2ξ__i=β__i∀i,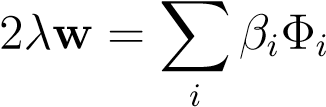 (10.11)
(10.11)
Plugging it back into the Lagrangian, we obtain the dual Lagrangian,
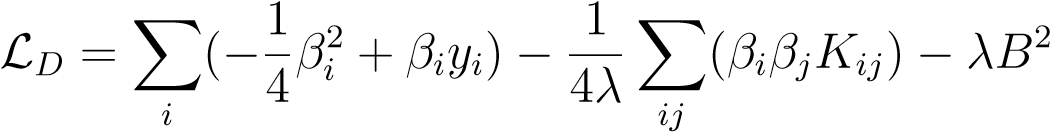 (10.12)
(10.12)
We now redefineα__i=βi/(2λ)to arrive at the following dual optimization problem,
maximize−α,λ−λ_2Xαi2+2λXαiyi−λXαiαjK_ij−λB_2_s.t.λ≥ 0
_i_iij
(10.13) Taking derivatives w.r.t.αgives precisely the solution we had already found,
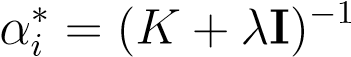 y(10.14)
y(10.14)
Formally we also need to maximize overλ. However, different choices ofλ_correspond to different choices for_B. Eitherλ_or_B_should be chosen using crossvalidation or some other measure, so we could as well varyλ_in this process.
CHAPTER10. KERNELRIDGEREGRESSION
One big disadvantage of the ridge-regression is that we don’t have sparseness in theαvector, i.e. there is no concept of support vectors. This is useful because when we test a new example, we only have to sum over the support vectors which is much faster than summing over the entire training-set. In the SVM the sparseness was born out of the inequality constraints because the complementary slackness conditions told us that either if the constraint was inactive, then the multiplier_α__i_was zero. There is no such effect here.
Chapter 11