8.1The Non-Separable case
Obviously, not all datasets are linearly separable, and so we need to change the formalism to account for that. Clearly, the problem lies in the constraints, which cannot always be satisfied. So, let’s relaxthose constraints by introducing “slack variables”,ξ__i,
| wTxi−b≤ −1 +ξ__i | ∀y__i= −1 | (8.19) |
|---|---|---|
| wTxi−b≥ +1 −ξ__i | ∀y__i= +1 | (8.20) |
| ξ__i≥ 0 ∀i | (8.21) |
The variables,ξ__i_allow for violations of the constraint. We should penalize the objective function for these violations, otherwise the above constraints become void (simply always pickξivery large). Penalty functions of the form_C(P_iξ_i)k_will lead to convex optimizationproblems for positive integers_k. Fork= 1,_2it is still a quadratic program (QP). In the following we will choose_k= 1._C_controls the tradeoff between the penalty and margin.
To be on the wrong side of the separating hyperplane, a data-case would needviolations are and is an upper bound on the number of violations.Pξi>1. Hence, the sum_iξ__i_could be interpreted as measure of how “bad” the
The new primal problem thus becomes,
minimizew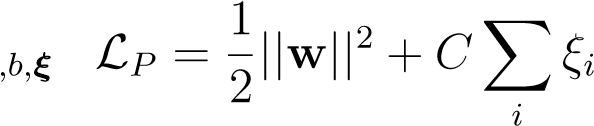
| subject to | y__i(wTxi−b) − 1 +ξ__i≥ 0 ∀i | (8.22) |
|---|---|---|
| ξ__i≥ 0 ∀i | (8.23) |
leading to the Lagrangian,
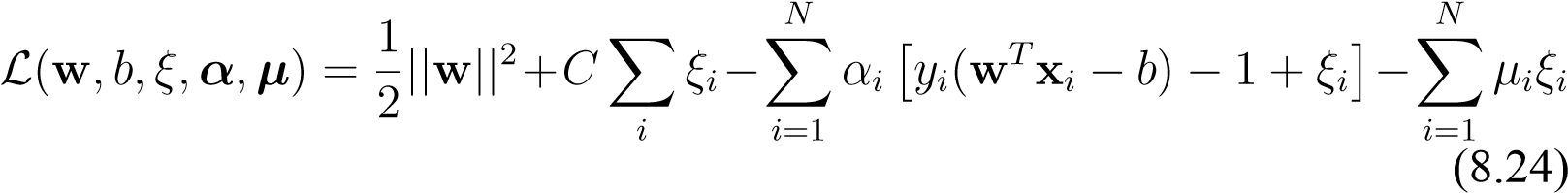
from which we derive the KKT conditions,
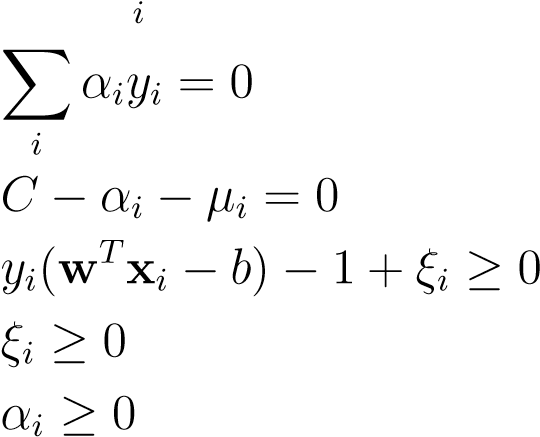 1.∂wLP= 0 →w−Xαiy__ixi= 0(8.25)
1.∂wLP= 0 →w−Xαiy__ixi= 0(8.25)
2.∂__b_L_P= 0 →(8.26)
3.∂__ξ_L_P= 0 →(8.27)
4_._constraint-1(8.28)
5_._constraint-2(8.29)
6_._multiplier condition-1(8.30)
7._multiplier condition-2µ_i≥ 0(8.31)
8_._complementary slackness-1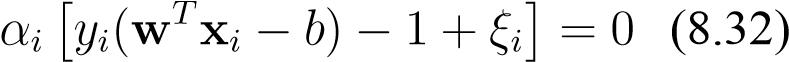
9._complementary slackness-1µiξ_i= 0(8.33)
(8.34)
From here we can deduce the following facts. If we assume thatξi>_0, thenµi= 0(9), henceαi=_C(1) and thusξ__i= 1 −y__i(xi__Tw−b)(8). Also, whenξ__i= 0we haveµi>_0(9) and henceαi< C. If in addition toξi_= 0we also have that_yi(w_Txi−b) − 1 = 0, thenαi>_0(8). Otherwise, if_y__i(wTxi−b) − 1_>_0
8.1. THENON-SEPARABLECASE
thenα__i= 0. In summary, as before for points not on the support plane and on the correct side we haveξ__i=α__i= 0(all constraints inactive). On the support plane, we still haveξ__i= 0, but nowαi>_0. Finally, for data-cases on the wrong side of the support hyperplane theαimax-out toαi=_C_and theξi_balance the violation of the constraint such that_yi(w_Txi−b) − 1 +ξ__i= 0.
Geometrically, we can calculate the gap between support hyperplane and the violating data-case to beξi/||w||. This can be seen because the plane defined byy__i(wTx−b) − 1 +ξ__i= 0is parallel to the support plane at a distance|1 +yib−ξ__i|/||w||from the origin. Since the support plane is at a distance|1 +yib|/||w||the result follows.
Finally, we need to convert to the dual problem to solve it efficiently and to kernelise it. Again, we use the KKT equations to get rid ofw,b_andξ_,
maximize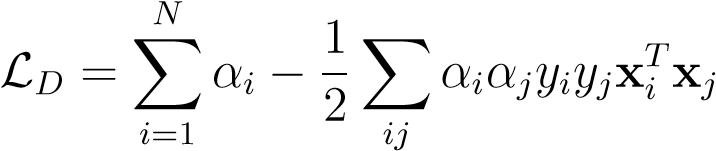
| subject to | αiy__i= 0 | (8.35) |
|---|---|---|
Surprisingly, this is almost the same QP is before, but with an extra constraint on the multipliersα__i_which now live in a box. This constraint is derived from the fact thatαi=_C−_µiandµ_i≥ 0. We also note that it only depends on inner productsx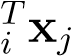 which are ready to be kernelised.
which are ready to be kernelised.
46CHAPTER8. SUPPORTVECTORMACHINES
Chapter 9