13.1Kernel Fisher LDA

So how do we kernelize this problem?Unlike SVMs it doesn’t seem the dual problem reveal the kernelized problem naturally. But inspired by the SVM case we make the following key assumption,

w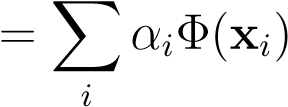(13.13)

CHAPTER13. FISHERLINEARDISCRIMINANTANALYSIS

This is a central recurrent equation that keeps popping up in every kernel machine. It says that although the feature space is very high (or even infinite) dimensional, with a finite number of data-cases the final solution,w∗, will not have a component outside the space spanned by the data-cases. It would not make much sense to do this transformation if the number of data-cases is larger than the number of dimensions, but this is typically not the case for kernel-methods. So, we argue that although there are possibly infinite dimensions available a priori, at mostN_are being occupied by the data, and the solutionwmust lie in its span. This is a case of the “representers theorem” that intuitivelyreasons as follows. The solutionwis the solution to some eigenvalue equation,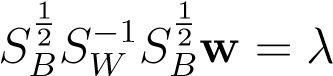w, where both_SB_and_SW(and hence its inverse) lie in the span of the data-cases. Hence, the partw⊥that is perpendicular to this span will be projected to zero and the equation above puts no constraints on those dimensions. They can be arbitrary and have no impact on the solution. If we now assume a very general form of regularization on the norm ofw,then these orthogonal components will be set to zero in the final solution:w⊥= 0.

In terms ofαthe objectiveJ(α)becomes,

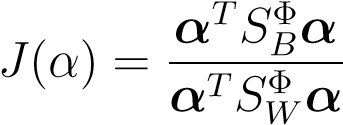(13.14)

where it is understood that vector notation now applies to a different space, namely the space spanned by the data-vectors,RN. The scatter matrices in kernel space can expressed in terms of the kernel only as follows (this requires some algebra to

verify),

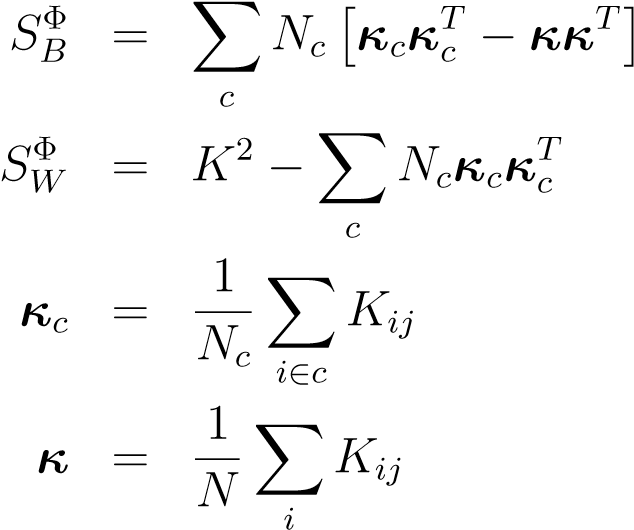(13.15)

(13.16)

(13.17)

(13.18)

So, we have managed to express the problem in terms of kernels only which is what wewere after. Note that since the objective in terms ofαhas exactly the same form as that in terms ofw, we can solve it by solving the generalized

13.2. ACONSTRAINEDCONVEXPROGRAMMINGFORMULATIONOFFDA67

eigenvalue equation. This scales as_N_3which is certainly expensive for many datasets. More efficient optimization schemes solving a slightly different problem and based on efficient quadratic programs exist in the literature.

Projections of new test-points into the solution space can be computed by,

wTΦ(x) = XαiK(xi__,x)(13.19)

i

as usual. In order to classify the test point we still need to divide the space into regions which belong to one class. The easiest possibility is to pick the cluster

with smallest Mahalonobis distanc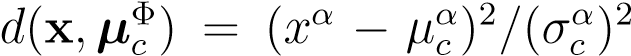e:where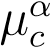

and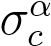represent the class mean and standard deviation in the 1-d projected space respectively. Alternatively, one could train any classifier in the 1-d subspace.

One very important issue that we did not pay attention to is regularization. Clearly, as it standsthe kernel machine will overfit. To regularize we can add a term to the denominator,

S__W→S__W+βI(13.20)

By adding a diagonal term to this matrix makes sure that very small eigenvalues are bounded away from zero which improves numerical stability in computing the inverse. If we write the Lagrangian formulation where we maximize a constrained quadratic form inα, the extra term appears as a penalty proportional to||α||2which acts as a weight decay term, favoring smaller values ofαover larger ones. Fortunately, the optimizationproblem has exactly the same form in the regularized case.

13.2 A Constrained Convex Programming Formulation of FDA

68CHAPTER13. FISHERLINEARDISCRIMINANTANALYSIS

Chapter 14