55

CHAPTER11. KERNELK-MEANSANDSPECTRALCLUSTERING

definitions you can now check that the matrixPM_defined as,_L=diag[1/nZ__nk] =diag[1/N__k]. Finally defineΦin=φ__i(x__n). With these

M= ΦZLZ__T(11.5)

consists ofN_columns, one for each data-case, where each column contains a copy of the cluster meanµ__k_to which that data-case is assigned. Using this we can write out the K-means cost as,

C=tr(Φ −M)(Φ −M)T

Next we can show thatZTZ=L−1(check this), and thus that(ZLZ__T)2=ZLZ__T. In other words, it is a projection. Similarly,I−_ZLZ__T_is a projection on the complement space. Using this we simplify eqn.11.6 as,

C=tr[Φ(I−ZLZ__T)2ΦT]	(11.7)
=tr[Φ(I−ZLZ__T)ΦT]	(11.8)
=tr[ΦΦT] −tr[ΦZLZ__TΦT]	(11.9)
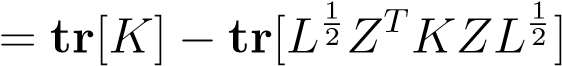	(11.10)

where we used thattris defined as taking the square root of the diagonal elements.

Note that only the second term depends on the clustering matrix Z, so we can we can now formulate the following equivalent kernel clustering problem,

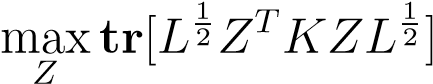(11.11)

such that:_Z_is a binary clustering matrix.(11.12)

This objective is entirely specified in terms of kernels and so we have once again managed to move to the ”dual” representation. Note also that this problem is very difficult to solve due to the constraints which forces us to search of binary matrices.

Ournext step will be to approximate this problem through a relaxation on this constraint. First we recall that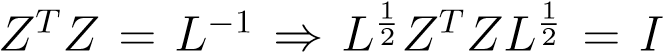. Renaming

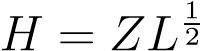, withH_an_N×_K_dimensional matrix, we can formulate the following relaxation of the problem,

57

Note that we did not require_H_to be binary any longer. The hope is that the solution is close to some clustering solution that we can then extract a posteriori.

The above problem should look familiar. Interpret the columns of_H_as a collection of_K_mutually orthonormal basis vectors. The objective can then be written as,

K

XhTkKhk(11.15)

k=1

By choosingh_k_proportional to the_K_largest eigenvectors of_K_we will maximize the objective, i.e. we have

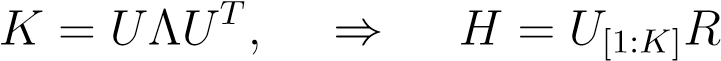(11.16)

whereR_is a rotation inside the eigenvalue space,_RR__T=RTR=I. Using this you can now easily verify thattr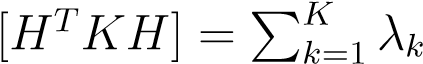where{λ__k}, k= 1_..K_are the largest K eigenvalues.

What is perhaps surprising is that the solution to this relaxed kernel-clustering problem is givenby kernel-PCA! Recall that for kernel PCA we also solved for the eigenvalues ofK. How then do we extract a clustering solution from kernel-PCA?

Recall that the columns ofH(the eigenvectors ofK) should approximate the binary matrixZ_which had a single1per row indicating to which cluster data-case_n_is assigned. We could try to simply threshold the entries of_H_so that the largest value is set to1and the remaining ones to0. However, it often works better to first normalize_H,

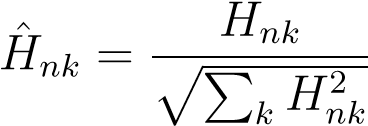(11.17)

All rows ofHˆare located on the unit sphere. We can now run a simple clustering algorithm such as K-means on the data matrixHˆto extract K clusters. The above procedure is sometimes referred to as “spectral clustering”.

Conclusion: Kernel-PCA can be viewed as a nonlinear feature extraction technique. Input is a matrix of similarities (the kernel matrix or Gram matrix) which should be positive semi-definite and symmetric. If you extract two or three features (dimensions) you can use it as a non-linear dimensionalityreduction method (for purposes of visualization). If you use the result as input to a simple clustering method (such as K-means) it becomes a nonlinear clustering method.

58CHAPTER11. KERNELK-MEANSANDSPECTRALCLUSTERING

Chapter 12